Andrew H. Fagg
This assignment focuses on the population code interpretation of neural activity. It is a pen-and-paper exercise and should require at most 2 hours to complete (including writing time). It is due at 5 pm on Tuesday, October 2nd.
Figure 1 depicts a two-joint robot (or monkey) arm. The
forward kinematics define the relationship between the arm's position
in joint space (
![]() )
and the
endpoint of the arm (
)
and the
endpoint of the arm (
![]() ). Specifically:
). Specifically:
| x | = | ||
| y | = |
The Jacobian, ![]() describes the local linear transformation
from joint velocities to Cartesian velocities:
describes the local linear transformation
from joint velocities to Cartesian velocities:
| = | |||
| = | ![$\displaystyle \left[
\begin{array}{cc}
\frac{\partial x}{\partial \theta_s} &
\...
...eft[
\begin{array}{c}
\dot{\theta_s} \\
\\
\dot{\theta_e}
\end{array}\right],$](img10.gif) |
where:
| = | |||
| = | |||
| = | |||
| = |
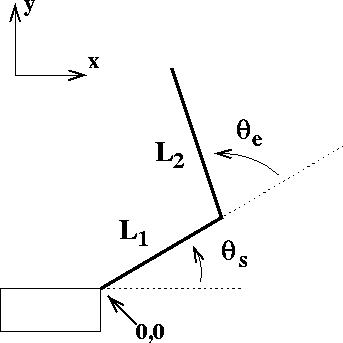 |
We will assume that
L1 = L2 = 1 and that a movement from a
starting point to a target is very small. The latter allows us to
assume that a movement can be expressed as an instantaneous velocity
(i.e. as ![]() and
and
![]() ).
).
Suppose that a cell in MI has a ``real'' preferred direction in
joint space of
![]() .
.
Question 1.1:
At position
![$\theta = \left[ {\frac{\pi}{4} \atop \frac{\pi}{2}}
\right]$](img27.gif) , what is the apparent preferred direction in Cartesian space?
, what is the apparent preferred direction in Cartesian space?
Answer:
![$\dot{X} = \left[ {-\frac{\sqrt{2}}{2} \atop \frac{\sqrt{2}}{2}}
\right]$](img28.gif)
Question 1.2:
At position
![$\theta = \left[ {0 \atop \frac{\pi}{2}}
\right]$](img29.gif) , what is the cell's apparent preferred direction?
, what is the cell's apparent preferred direction?
Answer:
![]()
Suppose an MI cell has a ``real'' preferred direction of
![]() .
.
Question 1.3:
At position
![$\theta = \left[ {\frac{\pi}{4} \atop \frac{\pi}{2}}
\right]$](img32.gif) , what is the apparent preferred direction in joint space?
, what is the apparent preferred direction in joint space?
Answer:
![$\dot{\theta} = \left[ {-\frac{1}{\sqrt{2}} \atop 0}
\right]$](img33.gif)
Question 1.4:
At position
![$\theta = \left[ {0 \atop \frac{\pi}{2}}
\right]$](img34.gif) , what is the cell's apparent preferred direction in joint space?
, what is the cell's apparent preferred direction in joint space?
Answer:
![]()
The model for cell discharge used by Georgopolous et al. was:
| (1) |
where ![]() is the cell discharge rate,
is the cell discharge rate,
![]() is the direction of movement in Cartesian space and a,
b, and
is the direction of movement in Cartesian space and a,
b, and
![]() are parameters.
are parameters.
Question 1.5:
Construct an equivalent model for a cell that encodes movement in
joint coordinates. In other words, give an expression for the cell
discharge rate as a function of
![]() and
and
![]() .
Note that there is not a unique answer.
.
Note that there is not a unique answer.
| = | (2) |
Georgopolous' ``cosine tuning function'' is but one way to describe
the transformation of a distance metric (in this case
![]() )
into a cell discharge rate. It
happens to be very convenient because relative orientation and the
cosine function are both periodic in nature. But - it does not have
to be this way...
)
into a cell discharge rate. It
happens to be very convenient because relative orientation and the
cosine function are both periodic in nature. But - it does not have
to be this way...
Suppose that instead of coding movement direction, we would like to encode a description of object shape and size (e.g., as extracted by the visual system). The shapes and parameters that we would like our population of cells to encode are:
| Shape | Parameters |
| sphere | diameter |
| cylinder | diameter, length |
| box | length, width, height |
Question 1.6:
Give one possible population coding scheme for this set of objects.
In other words, for the set of cells, write an expression (or
expressions) representing the cells' discharge rate as a function of
the exact object being coded.
One Answer: Assume that there are three separate populations of neurons -
one for each of the different shapes. For any particular shape, only
those cells that encode that shape will be active.
For sphere cells:
| dis(diam) | = | ai + bi Gi(diam - diampref,i). |
For cylinder cells:
| dic(diam, len) | = | ai + bi Gi(diam - diampref,i) + ci Gi(len - lenpref,i) . |
For box cells:
| dib(len, width, height) | = | ai + bi Gi(len - lenpref,i) + ci Gi(width - widthpref,i) | |
| + fi Gi(height - heightpref,i) . |
Where Gi() is Gaussian in shape:
| Gi(x) | = |
Another Answer: same as above, but with multidimensional Gaussians.
For sphere cells:
| dis(diam) | = | ai + bi Gi(diam - diampref,i). |
For cylinder cells:
| dic(diam, len) | = | ![$\displaystyle a_i
+ b_i G_i \left( \left [ {diam - diam_{pref,i}} \atop {len -
len_{pref,i}} \right ] \right ).$](img46.gif) |
For box cells:
| dib(len, width, height) | = | ![$\displaystyle a_i + b_i
G_i\left( \left[ \begin{array}{c}
{len - len_{pref,i}} ...
... - width_{pref,i}} \\
{height - height_{pref,i}}
\end{array}\right ] \right) .$](img47.gif) |
Where Gi() is Gaussian in shape:
| Gi(x) | = | 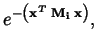 |
and where Mi is a scaling matrix.
This document was generated using the LaTeX2HTML translator Version 98.1p1 release (March 2nd, 1998)
Copyright © 1993, 1994, 1995, 1996, 1997, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -no_navigation -split 0 -t CMPSCI/NSB 691C: HW1 -dir html -no_reuse -tmp /tmp hw1.tex.
The translation was initiated by Andrew H. Fagg on 2001-10-04