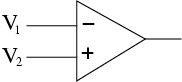
Op amps are versatile ICs containing a hundred or so transistors that can perform a vareity of mathematical functions. For this reason, they are the building blocks of many signal processing circuits. They have two inputs, an inverting (-) and noninverting (+). A positive voltage source and negative voltage source or ground are connected directly to the op amp, although these are rarely shown on circuit diagrams. There is a single output, which is almost always connected to the inverting input with a negative feedback loop.

All of the example circuits can be analyzed by observing the following simple rules.
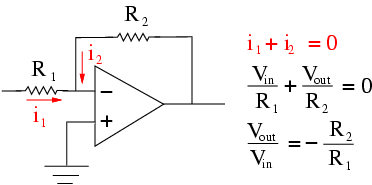
Inverting Amplifier - This configuration copies an inverted and scaled version of the input signal to its output. In doing so, the circuit isolates the circuit that produces the input reference from the circuit that uses the output by virtue of our op amp's impedance relationships.
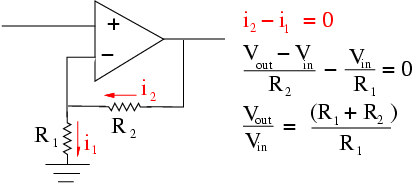
Non-Inverting Amplifier - We can accomplish amplification without inversion if we re-configure the circuit slightly.
By setting R2 to zero (short circuit) and R1 to infinity (open circuit to ground), we get a non-inverting, unity gain amplifier - the unity-gain follower. This is an important use of operational amplifiers. The high input impedance of the amp draws virtually no current and so acts as an impedance buffer. One could, for instance, use a voltage divider to step the voltage used to drive a resistive load down without worrying about impedance loading the divider. The op amp lets you track the input voltage without drawing significant current.
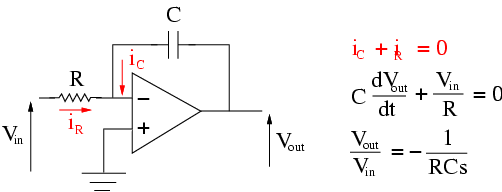
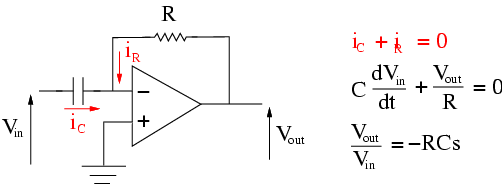
Integrating and Differentiating Amplifiers - By using a capacitance, the op amp can compute the integral and differential of the input voltage. In the first example, we see that the output voltage is the integral of the input voltage.
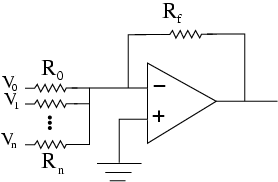
Adder - This circuit produces and output equal to the negative weighted sum of the respective inputs. One can imagine that with the right input resistances, we could construct a form of D/A converter with in which input "bits" are amplified by an amount proportional to their position in a binary word.
Comparator - This setup is used to determine which input signal is greater. When the inputs are equal, there is no output. When the inverting input is greater, the op amp becomes saturated and output voltage is equal to the positive voltage supply. When the inverting input is greater, the output voltage is equal to the negative voltage supply. There are TTL comparators available that would be recommended for this purpose, but the mighty op amp can do it in a pinch.