 |
Andrew H. Fagg1 - Andrew G. Barto1 - James C. Houk2
{fagg | barto}@cs.umass.edu houk@casbah.acns.nwu.edu
1Department of Computer Science 2Department of Physiology
University of Massachusetts Northwestern University School of Medicine
Amherst, MA 01003-4610 Chicago, IL 60611-3008
When infants begin to perform goal-directed reaching between approximately 4 and 5 months-of-age, the kinematics of their reaches show multiple accelerations and decelerations of the hand, which appear to reflect a correcting series of submovements. Although each submovement is an inaccurate correction, the sequence of submovements is often successful in reaching the target. By what process does the infant's reach controller come to eventually produce adult-like reaching behavior, characterized by bell-shaped velocity profiles and only occasional corrections? We suggest that motor command parameters are tuned in a supervised learning fashion using training information derived from proprioceptive feedback received during corrective movements. Although this is not high-quality training information, it is sufficient to tune motor command parameters in order to bring a dynamic arm quickly and accurately to the target, as we show in a series of simulations. We also suggest that additional parameters can be tuned to satisfy constraints other than end-point constraints through a reinforcement learning process.
When infants begin to perform goal-directed reaching between approximately 4 and 5 months-of-age, the kinematics of their reaches show multiple accelerations and decelerations of the hand, which appear to reflect a correcting series of submovements. Although each submovement is an inaccurate correction, the sequence of submovements is often successful in reaching the target [von Hofsten, 1979,Berthier, 1997]. By the end of the second year of life, most infants show fairly smooth and precise movements toward targets.
These and other observations made by researchers studying the development of human motor control raise many questions about the mechanisms involved in the acquisition of motor skills. Although control engineering, especially its use in robotics, provides essential help in understanding a range of possibilities, we know of no conventional control architecture that is consistent with what developmental psychologists know about human motor development. In this paper, we describe a model of the development of reaching that is informed by salient features of infant motor development, as well as by features of biological motor control in general.
Key aspects of our model are the following: 1) submovements are generated by motor commands characterized by relatively few parameters, so that no detailed trajectory planning is employed; 2) trajectory details are strongly influenced by the motor plant, which includes muscles and spinal reflexes with important nonlinear properties; 3) there is a built-in ability to make target-directed movements, but this ability is initially extremely crude; and 4) learning depends on several types of learning feedback, including proprioceptive feedback generated during corrective movements as well as evaluative feedback assessing the overall quality of movements with respect to multiple criteria. This implies that learning is a combination of supervised learning and reinforcement learning (RL). Additionally, the model has connections to a developing model of how the cerebellum and other brain structures are involved in regulating movement (e.g., Houk and Barto, 1992; Houk et al., 1996; Barto et al., submitted), although we do not have the space to describe these connections here. We present results of our initial efforts to assess the computational plausibility of these features.
When adults reach in the horizontal plane to specified targets, several regularities are observed in the trajectory of the hand. First, the hand speed exhibits a smooth, bell-shaped profile, and when accuracy requirements are low, the profile is symmetric about its peak. Second, the hand follows a nearly straight path between the initial and target positions. These regularities have been interpreted by many to mean that prior to movement execution, a detailed trajectory of the movement is planned and then transformed into a time series of muscle activation patterns that produce the desired movement (e.g., Kawato et al., 1987; Kawato and Gomi, 1993; Schweighofer, 1995). Another possibility, which we explore here, is that the regularities are due in part to the dynamical properties of the limb and muscle, and that a controller need only specify a small number of control parameters. Furthermore, a controller need not explicitly represent an explicit plan of the desired behavior prior to movement execution, e.g., a trajectory in Cartesian or joint space.
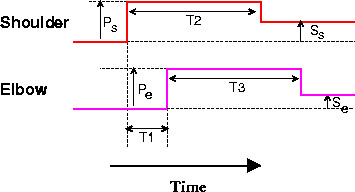
One minimal representation of a two-joint reach controller consists of a pair of pulse-step joint commands (Figure 1). The pulse component of the command is responsible for initiating movement of a joint; the step specifies a region (not a unique point) in which the joint will stop moving. Pulse-step control is known to be used in the generation of rapid eye movements [Robinson, 1975] and has been suggested as a reasonable approximation for limb movement control in cat [Ghez, 1979,Ghez and Martin, 1982]. In the model, the control outputs are specified by a set of seven parameters: the pulse and step heights for the shoulder and elbow (Ps, Pe, Ss, Se), the length of the shoulder and elbow pulses (T2 and T3), and the relative onset time of the two pulses (T1). These pulse-step commands are generated in a purely open-loop mode only for the sake of simplicity. In a more realistic model, the commands could be influenced by appropriately delayed feedback (Barto et al., submitted).
 |
The motor plant is a simulated, two degree-of-freedom, planar arm. The
dynamic parameters were selected to be consistent with an adult
arm (Gribble et al., 1998).
The shoulder and elbow joints are actuated by
two pairs
of opposing muscles. The muscle model combines a Hill-based lumped
parameter model [Winters, 1990] with aspects of Feldman's
![]() -model (Feldman, 1966; Gribble et al., 1998),
and includes a
nonlinear damping term mediated by the stretch reflex, as
described by Gielen and Houk (1984, 1987) and Wu et al. (1990).
The voluntary pulse-step commands set the reflex thresholds for each
pair of muscles. For a given motor signal, the two opposing muscles
produce a unique joint equilibrium position. However, nonlinear dynamics of
the stretch reflex create a stiction region around the
equilibrium. Once the joint enters this region, it slows rapidly,
effectively halting the joint's movement. This formulation of
muscle/reflex dynamics has the advantage of removing from the controller's
responsibility the
generation of braking bursts of muscle activity to halt movement.
In effect, the stretch reflex generates braking antagonist activity.
This formulation also allows rapid movements while limiting the potential
for oscillations about the
endpoint. More details of the muscle/reflex model may be found
in Barto et al. (submitted) and Fagg et al. (1998).
-model (Feldman, 1966; Gribble et al., 1998),
and includes a
nonlinear damping term mediated by the stretch reflex, as
described by Gielen and Houk (1984, 1987) and Wu et al. (1990).
The voluntary pulse-step commands set the reflex thresholds for each
pair of muscles. For a given motor signal, the two opposing muscles
produce a unique joint equilibrium position. However, nonlinear dynamics of
the stretch reflex create a stiction region around the
equilibrium. Once the joint enters this region, it slows rapidly,
effectively halting the joint's movement. This formulation of
muscle/reflex dynamics has the advantage of removing from the controller's
responsibility the
generation of braking bursts of muscle activity to halt movement.
In effect, the stretch reflex generates braking antagonist activity.
This formulation also allows rapid movements while limiting the potential
for oscillations about the
endpoint. More details of the muscle/reflex model may be found
in Barto et al. (submitted) and Fagg et al. (1998).
In the sections that follow, we describe two algorithms for setting the pulse-step parameters such that the target is accurately reached and a path straightness criterion is satisfied.
Berthier et al. (1993) suggested that proprioceptive feedback from individual corrective movements could provide information as to how to update previously-generated movements. Suppose that a movement is unsuccessful at reaching the target, which results in the generation of a corrective movement. The direction of the corrective movement (as measured by either the muscle activation pattern, or indirectly via proprioceptive afferents) provides training information to the controller as to how it should update its parameters for the preceding movement. Importantly, the corrective movements do not have to be accurate; they only need to move the hand, on the average, closer to the target. This can be done, as we describe below, without any consideration of the arm's dynamics.
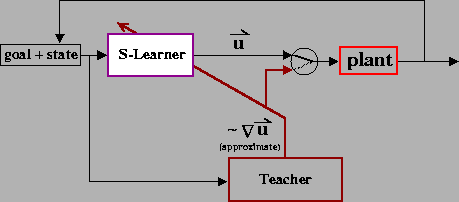 |
A particular implementation of this approach is illustrated in Figure 2. The behavioral protocol is as follows: the arm is placed in an initial configuration, and a target location is presented. As a function of this information, the Supervised Learning module (S-Learner) selects the pulse heights (Ps and Pe). The remaining parameters are held fixed: T1 = 0, T2 = T3 = 150msec, and Ss and Se are selected such that the joint equilibrium position is aligned with the target. Note that setting the step heights in this manner does not require knowledge of the arm dynamics, nor does this guarantee that the arm will stop at the target, due to the stiction behavior of the opposing muscles. The pulse-step commands are then executed, and the arm is allowed to come to rest. If the arm stops moving at a point far from the target, then the Teacher produces pulses of muscle activity, resulting in a sequence of corrective movements that bring the arm to the target. These pulses are also used to update the pulse parameters specified by the S-Learner. If the teacher produces a correction that primarily involves flexion of the elbow, for example, then the elbow pulse height (Pe) is increased in magnitude. On subsequent trials, this has the effect of producing a larger elbow flexion movement (or a smaller extension movement). Reaching trials are repeated until the S-Learner is able to reach the target without requiring correction.
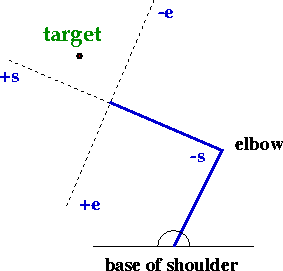
The pulses generated by the Teacher are fixed duration, with magnitudes that are selected heuristically. Karst and Hasan (1991) showed that a relatively simple rule could be used to describe the initial recruitment of arm muscles as a function of the position of the target relative to the hand, without taking into account the dynamics of the arm. In the model, the relative activation level of the shoulder and elbow muscles is derived from the target's position in a visual coordinate system with origin at the wrist and aligned along the forearm (Figure 3). Target locations along the forearm axis are translated into pure shoulder movements, whereas those located along the perpendicular axis result in pure elbow movements. Off-axis targets recruit a mixture of shoulder and elbow muscles.
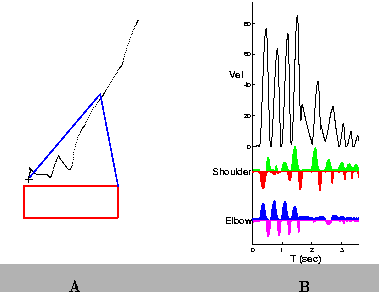
Prior to learning, the Teacher is responsible for producing all movements, as illustrated in Figure 4A. The initial position of the arm is located in the top-right corner of the workspace; the target is indicated by the ``+''. The path followed by the wrist is shown by the series of dots from the initial position to the target. Areas of high dot density indicate regions in which the arm slowed. Figure 4B shows the the hand speed profile (Vel), and the muscle activation patterns for the Shoulder and Elbow. After 40 repetitions of the same reach, the Supervised Learning controller has discovered a set of pulse parameters that brings the arm to the target without the need for corrections (Figure 5). In addition, the hand speed profile is smooth and has a single peak.
 |
 |
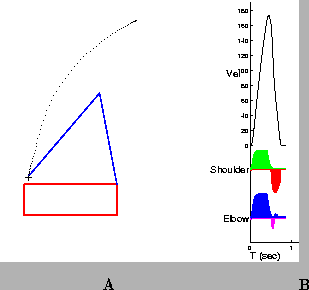 |
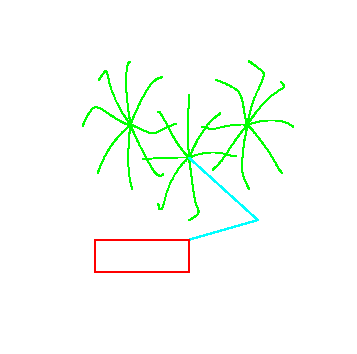
Figure 6 demonstrates the post-learning behavior of the arm for a variety of initial and target positions. For each initial/target pair, the pulse parameters were learned independently (no mechanism has been implemented for generalization across similar reaches, although this is a straightforward extension of the model). Note that many of the paths contain ``hooks'' near the end of movement. In each of these cases, one joint (typically the shoulder) has completed its motion long before the other. In addition, the hooked paths typically exhibit two peaks in the hand speed profile.
 |
The undesirable aspects of the trajectories described above can be addressed by adjusting additional pulse-step parameters (specifically, T1 and T3 of Figure 1). The critical question is how to best select these parameters given the observed behavior of the arm on one or more trials. It is possible to address the ``hooking problem'' by extending the supervised learning method in the following manner. If the arm reaches the target without correction, but the shoulder completes its motion before (after) the elbow, then T3 is increased (decreased) by a fixed duration. If T3is updated, then another trial is executed, and the pulse-step parameters (Ps, Pe, and T3) are adjusted as necessary.
Although this heuristic method can minimize the observed hooking behavior, the resulting paths are approximately straight in joint space, which implies that the paths are often significantly curved in Cartesian space. Hollerbach and Atkeson (1987) suggested that approximately straight Cartesian movements can be achieved by staggering the onset of joint movement, which can be accomplished in this model by adjusting the T1 parameter. However, it is not apparent that there is a simple rule for extracting a direction of adjustment of the T1 parameter from the observed behavior of the arm on a single trial (specifically, the straightness of the path). While we could in principle compute the appropriate Jacobian from a model of the arm (cf. Jordan et al., 1994), it is much simpler to use an RL-type search process to discover the T1 that results in the straightest hand path.
One possible architecture is shown in Figure 7. Two
separate learning modules, the S-Learner and the R-Learner,
specify orthogonal components of the pulse-step controller
(specifically,
![]() and
and
![]() ).
The S-Learning module utilizes the method
described above to discover the appropriate uS for a given
situation, while in parallel, the R-Learning module makes use of an
RL approach [Sutton and Barto, 1998] to search for
the optimal uR.
).
The S-Learning module utilizes the method
described above to discover the appropriate uS for a given
situation, while in parallel, the R-Learning module makes use of an
RL approach [Sutton and Barto, 1998] to search for
the optimal uR.
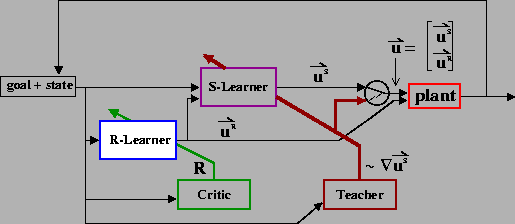 |
The learning protocol is as follows: For a given initial position and target, the R-Learning module selects a particular uR. As a function of the initial and target positions (and possibly uR), the S-Learning module selects a uS, and the motor signals are generated. If the target is not reached or the two joints do not complete their motions simultaneously, the Teacher provides a heuristic update to uS, and produces a sequence of corrective movements that bring the arm to the target. Reaching trials are repeated, with the same uR, until changes become sufficiently small. The resulting trajectory is evaluated by the Critic as a function of its deviation from the straight-line path between the initial and target positions (the reward, R, is highest for no deviation from the straight path). Based upon this evaluation, the R-Learner selects a new uR, and the supervised learning process is repeated. An important distinction between these two learning systems is that the Teacher informs the S-Learner as to how to update its motor signal, whereas the Critic only provides an evaluation of the resulting behavior and not a directional change to the R-Learner's motor signal.
For the experiments described below, the R-Learner makes use of a hierarchical search in order to discover the appropriate uR. At the first level of the search, a coarse sampling of T1's are evaluated. The best performing T1 (maximum R) becomes the center of the search at the next level, around which a finer sampling of T1's are selected. This process is repeated until the finest granularity is reached.
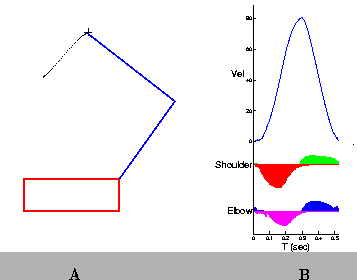 |
In practice, between 200 and 700 movement trials are required to find the appropriate set of parameters for a single starting point/target pair. The resulting paths are often nearly straight, and the velocity profiles are smooth and exhibit single peaks. (Figures 8 and 9).
 |
Adult reaching movements exhibit regularities in the form of straight hand paths and smooth, bell-shaped hand speed profiles. To produce these regularities, in what form does the reach controller specify motor signals, and what training information is necessary to tune these signals with experience? In our model, the controller represents the motor signals by specifying the height and timing parameters of a pulse-step waveform for each joint, making no use of an explicit plan for the desired trajectory to be followed.
Despite the low dimensionality of the control signal representation, it is possible to produce regularities similar to those of adult reaches, due in part to the dynamical behavior of the muscles and the arm. This approach is similar to that of Karniel and Inbar (1997), a key difference being that only the agonist muscle bursts are specified directly in our model. The braking antagonist burst arises naturally from the stretch reflex built into our model. Their learning procedure also relies on a systematic variation of all of the control parameters to estimate an error gradient, in order to update control parameters.
Our model, on the other hand, assumes the existence of a crude mechanism for the generation of corrective movements. While it is easy to initiate movement in a generally correct direction, it is much harder to accurately reach a target endpoint with a fast and smooth movement. Our model shows that crude corrective movements not only allow successful reaching on every trial (although early reaches may require many corrections), but they can also provide training information useful for updating a subset of controller parameters so that faster and smoother movements result. This process produces a progression from multi-segmented reaches qualitatively similar to those of infants to more skillful reaches similar to those of adults. An additional RL mechanism adjusts pulse timing parameters so that the hand follows a relatively straight path. It would have been possible to use RL to adjust all of the controller's parameters, but this would have required a more difficult search in a higher-dimensional space. We think it is plausible that infants use RL to tune aspects their movements, although it is unlikely that they use a straightness criterion as we have done here. It is more likely that an infant's reinforcement function depends on factors such as movement time and accuracy.
Our learning approach is related to Kawato's feedback error learning in that learning is guided by movement produced by a feedback controller external to the learning module (Kawato et al., 1987; Kawato and Gomi, 1993; Schweighofer, 1995). Our model differs from this work in two respects. First, feedback in our model is not provided continuously, rather it is only available sporadically. Second, our model does not require the use of a high-quality reference trajectory from which the corrective movements are computed. Although Cartesian path information is used by the RL component in adjusting the pulse timing parameters, this information is utilized after the reaching movement, and not during its planning or execution.
Although the controller in the present model is purely open-loop and learns to perform a movement from a single position to a single target, the learning approach is more generally applicable at two levels. First, it is possible to learn the pulse-step parameters as a function of the current state of the arm and target position, allowing the model to learn reaching movements over the entire workspace. Second, in the context of a cerebellar learning model, it is possible to learn to combine contextual information, motor efference copy, and delayed sensory inputs in order to compute the outgoing motor commands in an on-line fashion (Fagg et al., 1997; Barto et al., submitted).
This document was generated using the LaTeX2HTML translator Version 98.1p1 release (March 2nd, 1998)
Copyright © 1993, 1994, 1995, 1996, 1997, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -split 2 -t Learning to Reach Via Corrective Movements -dir html -no_reuse -tmp /tmp/fagg yale.tex.
The translation was initiated by Andrew H. Fagg on 1999-04-27