Technical Report #00-03
Andrew H. Fagg
fagg@cs.umass.edu
Department of Computer Science
University of Massachusetts, Amherst
A muscle's action on a joint not only depends upon the muscle's size and activation level, but also upon the mechanical advantage (or moment arm) of the muscle upon the joint. This relationship is made more complex by the fact that the mechanical advantage can change drastically with skeletal configuration. Here, we describe a model of muscle geometry for several muscles involved in elbow and shoulder actuation. The model captures the gross changes in muscle moment arm while preserving reasonable computational efficiency which facilitates its use in simulation.
In constructing a model of muscle action on a limb, we ultimately wish
to compute the torques that are applied to the joints as a function of
the current state of the limb (as described by joint position and
velocity) and set of descending motor commands. In Fagg et al. (2001a)
we develop a model of muscle force production with the stretch reflex
intact. We then apply this model to the generation of elbow
movements (Fagg et al., 2001b).
The skeleto-muscular geometry is used in two distinct stages
of this latter work. First, in order to make use of the muscle model, it
is necessary to know the instantaneous change in muscle length. This
quantity can be computed by knowing how a muscle changes its length as
a function of changes in joint angles (i.e.
![]() ). Second, once forces are computed by the muscle
model, the application of torques about the various joints requires
knowledge of the muscle moment arms for each joint. For some muscles,
this moment arm is constant; in others, the moment arm varies as a
function of skeletal configuration.
). Second, once forces are computed by the muscle
model, the application of torques about the various joints requires
knowledge of the muscle moment arms for each joint. For some muscles,
this moment arm is constant; in others, the moment arm varies as a
function of skeletal configuration.
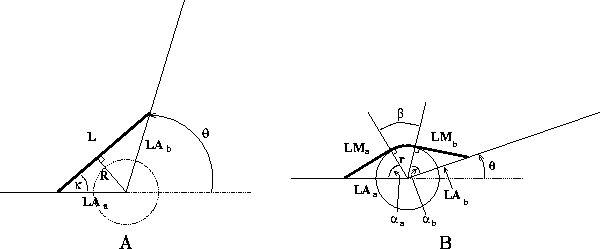
In order to compute both of these quantities, it is necessary to take into account the attachment points of the muscle to the skeletal structure, as well as the path that the muscle takes between these points. Winters and Stark (1988) suggested a simple model of path in which the muscle is assumed to follow a straight line between muscle origin and insertion, except for highly extended positions. In the latter case, the muscle is assumed to wrap around a spherical joint capsule whose center is also the joint's center of rotation (figure 1).
The work of Amis, Dowson, and Wright (1979) and others (1981) indicates that this form of path model captures the primary variation of muscle moment arms as a function of joint orientation for a number of elbow muscles, including the biceps long head and the triceps lateral head. In the latter case, however, the muscle wraps around the joint capsule for all feasible joint configurations, and hence the moment arm is assumed to be constant. Less is known about the geometry of muscles involving the shoulder, we assume for simplicity that this path model also applies in this case.
 |
In our model, we follow Gribble et al (1997, 1998) in making use of six equivalent muscles to drive movements of the shoulder and elbow. The primary muscle groups contributing to movements are assumed to be: the pectoralis (mono-articulate shoulder flexors), deltoid (shoulder extensors), biceps long head (mono-articulate elbow flexors), triceps lateral head (elbow extensors), biceps short head (bi-articulate flexors), and triceps long head (bi-articulate extensors). All three extensors are assumed to wrap around the associated joint capsule at all times. The mono-articulate shoulder and elbow flexors are assumed to follow the above path model, and the biarticulate flexor follows a two-joint generalization of this model (as has been done by Gribble 1998).
Note that for a given flexor muscle and joint, it can be shown for
both the wrap and no-wrap conditions that
![]() ,
where R is the muscle moment arm about the
joint.1 This relationship changes
sign for extensors. This leaves us with the task
of computing the muscle lengths and moment arms for both the
mono-articulate and bi-articulate flexor muscles, which we will do in
the following sections.
,
where R is the muscle moment arm about the
joint.1 This relationship changes
sign for extensors. This leaves us with the task
of computing the muscle lengths and moment arms for both the
mono-articulate and bi-articulate flexor muscles, which we will do in
the following sections.
The two conditions for the single-joint case are illustrated in figure 1. We first determine the joint boundary between these two cases, and then compute the necessary quantities for each condition.
The boundary between the wrap and no wrap conditions occurs where the muscle contacts the joint capsule at a single point, as illustrated in figure 2. The critical quantities are as follows:
where r is the radius of the joint capsule, and LAa and LAbare the distances from the muscle attachment points to the center of
joint rotation. ![]() is the joint angle at which the transition
between the two conditions occurs.
is the joint angle at which the transition
between the two conditions occurs. ![]() ,
,
![]() ,
LMa,
and LMb are constant properties of the triangles formed by the
center of rotation, the muscle attachment point, and the first point
at which the muscle contacts the joint capsule, and will be used for
the wrap condition.
,
LMa,
and LMb are constant properties of the triangles formed by the
center of rotation, the muscle attachment point, and the first point
at which the muscle contacts the joint capsule, and will be used for
the wrap condition.
The no-wrap condition applies if
![]() .
The
necessary quantities are computed as
follows (see Figure 1A):
.
The
necessary quantities are computed as
follows (see Figure 1A):
| L | = | 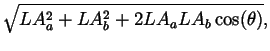 |
|
| = | 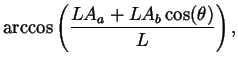 |
||
| R | = |
where R is the moment arm for the muscle about the joint.
| = | |||
| L | = | ||
| R | = | r, |
where ![]() ,
,
![]() ,
LMa, and LMb are computed in
equations 1-5.
,
LMa, and LMb are computed in
equations 1-5.
For the shoulder, less is known about the effective origin and
insertion for the muscle. We assume for the purposes of our model
that
![]() ,
,
![]() ,
and
,
and
![]() .
.
The biarticulate case, in which the muscle can wrap around both the shoulder and elbow joint capsules is a generalization of the single-joint case. However, we now have four separate cases to consider: whether or not the muscle wraps around each joint.
Figure 4 shows the basic structure of the model. Given
parameters: L1 (length of the upper-arm segment), r1 and r2 (the
radii of the shoulder and elbow joint capsules, respectively), and
LA1 and LA2 (the distance from the point of rotation to the
muscle attachment point); and the variables ![]() and
and ![]() (current orientation of the shoulder and elbow, respectively), we must
compute: R1 and R2 (the moment arms about the shoulder and
elbow), and L (the length of the muscle).
(current orientation of the shoulder and elbow, respectively), we must
compute: R1 and R2 (the moment arms about the shoulder and
elbow), and L (the length of the muscle).
The joint space is partitioned into four regions, as shown schematically in figure 5. The location of the boundaries depends upon the arm and muscle attachment parameters.
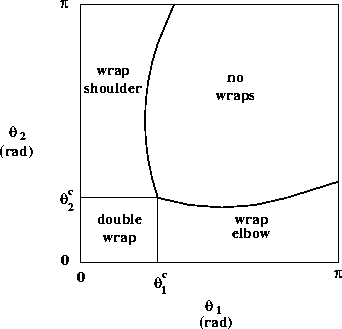 |
The most extreme point of the double-wrap region occurs when the muscle glances both joint capsules (figure 6). In other words, contact with each capsule is a single point, with no wrapping of the muscle. The associated quantities are computed as follows:
where
![]() and
and
![]() are the joint angles at which this
condition occurs. As long as
are the joint angles at which this
condition occurs. As long as
![]() and
and
![]() ,
the muscle wraps around both capsules.
LM1 and LM2 represent the distance from the muscle's point of
attachment to the corresponding joint capsule contact point; LMw is
the distance between the two contact points.
,
the muscle wraps around both capsules.
LM1 and LM2 represent the distance from the muscle's point of
attachment to the corresponding joint capsule contact point; LMw is
the distance between the two contact points.
The double-wrap condition exists if
![]() and
and
![]() .
.
As long as the double-wrap condition does not occur, and
![]() ,
then the possibility exists
that the muscle will wrap around the shoulder joint capsule. However,
the boundary varies as a function of
,
then the possibility exists
that the muscle will wrap around the shoulder joint capsule. However,
the boundary varies as a function of ![]() .
Therefore, the
strategy that we take is to assume no wrapping, compute the shoulder
moment arm, and then compare that moment arm to the radius of the
joint capsule. If R1 < r1, then we have the case in which the
muscle is wrapping around the shoulder joint capsule. These moment
arm computations for the no-wrap
condition are illustrated in figure 7. The process is
illustrated below:
.
Therefore, the
strategy that we take is to assume no wrapping, compute the shoulder
moment arm, and then compare that moment arm to the radius of the
joint capsule. If R1 < r1, then we have the case in which the
muscle is wrapping around the shoulder joint capsule. These moment
arm computations for the no-wrap
condition are illustrated in figure 7. The process is
illustrated below:
where <xa,ya> denotes the location of the muscle attachment to link 2 relative to the center of rotation of the shoulder, and R1and R2 are the moment arms.
Returning to the question of whether the muscle wraps around the
shoulder joint capsule - this is the case as long as
![]() and
and
![]() .
The latter condition is
necessary because when the shoulder is flexed to a large degree, the
moment arm drops below the r1 threshold, and yet the geometry is
such that the muscle does not wrap around the joint capsule.
.
The latter condition is
necessary because when the shoulder is flexed to a large degree, the
moment arm drops below the r1 threshold, and yet the geometry is
such that the muscle does not wrap around the joint capsule.
Determining the boundary for the elbow wrap case follows in the same
manner as the shoulder. Given that the double-wrap condition does not
apply, the elbow-wrap case applies if
![]() ,
,
![]() ,
and
,
and
![]() (where R2 is the same as in equation
17).
(where R2 is the same as in equation
17).
Refering to figure 7, the muscle length, L is simply:
| L | = | 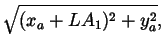 |
where xa and ya are from equations 14 and 15. The muscle moment arms are exactly what have been computed in equations 16 and 17.
The shoulder wrap case is illustrated in figure 8. The corresponding quantities are computed as follows:
| b | = | 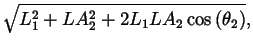 |
|
| = | 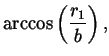 |
||
| = | 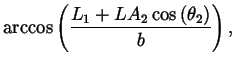 |
||
| = | |||
| = | 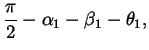 |
||
| L | = | ||
| R1 | = | r1, | |
| R2 | = |
where ![]() and LM1 are from equations 6 and
11, respectively.
and LM1 are from equations 6 and
11, respectively.
The elbow wrap case is illustrated in figure 9. The associated quantities are computed as follows:
| = | 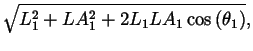 |
||
| = | 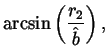 |
||
| = | 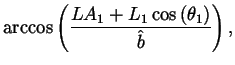 |
||
| = | 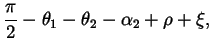 |
||
| L | = | 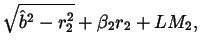 |
|
| R1 | = | ||
| R2 | = | r2, |
where ![]() and LM2 are from equations 7 and
12, respectively.
and LM2 are from equations 7 and
12, respectively.
| = | |||
| = | |||
| L | = | ||
| R1 | = | r1 | |
| R2 | = | r2 |
where ![]() ,
,
![]() ,
,
![]() ,
LM1, LM2, and LMw are
as computed in equations 6-13.
,
LM1, LM2, and LMw are
as computed in equations 6-13.
We use the following parameters for the biarticulate flexor:
| LA1 | = | ||
| LA2 | = | ||
| r1 | = | ||
| r2 | = | ||
| L1 | = |
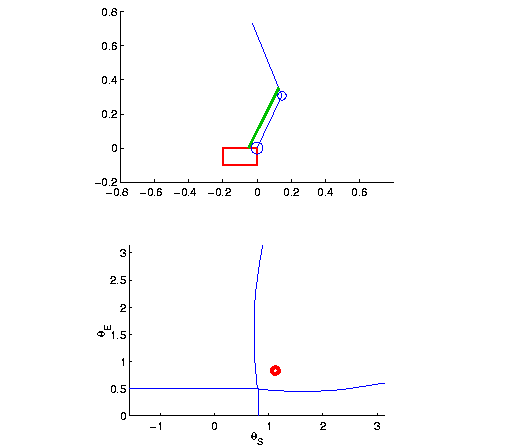
Figure 11 shows the arm and muscle in a no-wrap
configuration, and the joint space boundaries defined by the muscle
wrapping state. Variations of the muscle length and joint moment arms
are shown in figures 12 and 13. Note that
for both joints, at the extreme limits (
![]() for the left
panel, and
for the left
panel, and
![]() for the right panel), the moment arms become
negative. In these cases, the muscle applies torques in the
direction that is opposite from normal (for the biceps short head,
this situation cannot occur physically due to joint limit constraints,
however it is known to happen for other arm muscles).
for the right panel), the moment arms become
negative. In these cases, the muscle applies torques in the
direction that is opposite from normal (for the biceps short head,
this situation cannot occur physically due to joint limit constraints,
however it is known to happen for other arm muscles).
 |
In practice, we have found that it is more efficient to use the equations presented here to construct a lookup table for muscle length and moment arm as a function of joint angle(s) rather than using the equations directly during a dynamic simulation. We then perform interpolation using elements of the lookup table.
We assume that the extensors maintain a constant moment arm. The
monoarticulate shoulder and elbow muscles, we assume moment arms of
![]() and
and ![]() ,
respectively. For the biarticulate muscle,
we assume a moment arm of
,
respectively. For the biarticulate muscle,
we assume a moment arm of ![]() and
and ![]() for the shoulder and
elbow, respectively. These values are consistent
with those used by Gribble et al. (1998).
for the shoulder and
elbow, respectively. These values are consistent
with those used by Gribble et al. (1998).
This document was generated using the LaTeX2HTML translator Version 98.1p1 release (March 2nd, 1998)
Copyright © 1993, 1994, 1995, 1996, 1997, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -no_navigation -split 0 -t Moment Arm Model moment.tex.
The translation was initiated by Andrew H. Fagg on 2001-08-29